জ্যামিতির অন্যতম গুরুত্বপূর্ণ একটি আকৃতি হলো ট্রাপিজিয়াম। গণিত বা জ্যামিতি শিখতে গিয়ে শিক্ষার্থীদের মনে প্রায়ই প্রশ্ন জাগে, ট্রাপিজিয়াম কাকে বলে? সহজ কথায়, এটি এমন একটি চতুর্ভুজ যার আকৃতি অন্যান্য সাধারণ চতুর্ভুজ থেকে কিছুটা ভিন্ন। আজকের এই আর্টিকেলে আমরা ট্রাপিজিয়াম কাকে বলে, এর বৈশিষ্ট্য, প্রকারভেদ এবং অংক করার প্রয়োজনীয় সূত্রগুলো নিয়ে বিস্তারিত আলোচনা করব।
ট্রাপিজিয়াম কাকে বলে? (Definition of Trapezium)
যে চতুর্ভুজের একজোড়া বাহু সমান্তরাল কিন্তু অসমান, তাকে ট্রাপিজিয়াম (Trapezium) বলে।
অর্থাৎ, একটি ট্রাপিজিয়ামের চারটি বাহুর মধ্যে দুটি বাহু একে অপরের সমান্তরাল হবে (রেললাইনের মতো, যা কখনো মিলিত হয় না) এবং বাকি দুটি বাহু অসমান বা তীর্যক হবে। সমান্তরাল বাহু দুটিকে ট্রাপিজিয়ামের ‘ভূমি’ এবং ‘শীর্ষ’ বলা হয়, আর অসমান বাহু দুটিকে ‘তীর্যক বাহু’ বলা হয়।
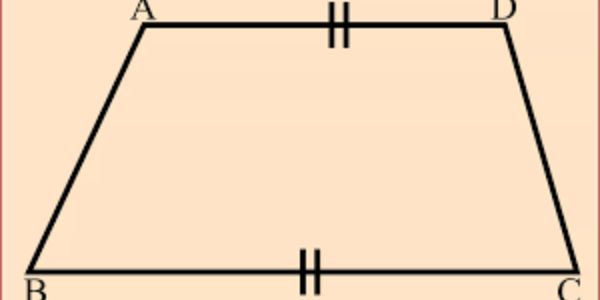
উদাহরণস্বরূপ: মনে করি, ABCD একটি চতুর্ভুজ। যদি এর AB বাহু এবং CD বাহু পরস্পর সমান্তরাল হয় ($AB \parallel CD$) কিন্তু সমান না হয়, তবে ABCD একটি ট্রাপিজিয়াম।
ট্রাপিজিয়ামের প্রধান বৈশিষ্ট্যসমূহ
ট্রাপিজিয়াম চেনার জন্য এর কিছু নির্দিষ্ট বৈশিষ্ট্য জানা প্রয়োজন। বৈশিষ্ট্যগুলো নিচে দেওয়া হলো:
১. ট্রাপিজিয়ামের চারটি বাহু থাকে, অর্থাৎ এটি একটি চতুর্ভুজ।
২. এর একজোড়া বিপরীত বাহু পরস্পর সমান্তরাল।
৩. অপর একজোড়া বিপরীত বাহু সমান্তরাল নয় (তীর্যক)।
৪. সমান্তরাল বাহুদ্বয়ের মধ্যবর্তী লম্ব দূরত্বকে ট্রাপিজিয়ামের উচ্চতা বলা হয়।
৫. ট্রাপিজিয়ামের চারটি কোণের সমষ্টি ৩৬০ ডিগ্রি বা ৪ সমকোণ।
৬. সমান্তরাল বাহুদ্বয়ের অন্তর্নিহিত কোণ দুটির সমষ্টি ১৮০ ডিগ্রি হয়।
ট্রাপিজিয়ামের প্রকারভেদ
বাহু এবং কোণের ওপর ভিত্তি করে ট্রাপিজিয়াম প্রধানত তিন প্রকার হতে পারে:
১. সমদ্বিবাহু ট্রাপিজিয়াম (Isosceles Trapezium):
যে ট্রাপিজিয়ামের অসমান বা তীর্যক বাহু দুটি পরস্পর সমান, তাকে সমদ্বিবাহু ট্রাপিজিয়াম বলে। এর ভূমিসংলগ্ন কোণ দুটিও পরস্পর সমান হয়।
২. সমকোণী ট্রাপিজিয়াম (Right-angled Trapezium):
যে ট্রাপিজিয়ামের যেকোনো একটি কোণ সমকোণ বা ৯০ ডিগ্রি, তাকে সমকোণী ট্রাপিজিয়াম বলে। এক্ষেত্রে একটি তীর্যক বাহু সমান্তরাল বাহুদ্বয়ের ওপর লম্ব হয়।
৩. বিষমবাহু ট্রাপিজিয়াম (Scalene Trapezium):
যে ট্রাপিজিয়ামের কোনো বাহুই সমান নয়, তাকে বিষমবাহু ট্রাপিজিয়াম বলে।
ট্রাপিজিয়ামের সূত্রাবলি (Formulas of Trapezium)
গণিতের সমস্যা সমাধানের জন্য ট্রাপিজিয়ামের ক্ষেত্রফল ও পরিসীমার সূত্র জানা অত্যন্ত জরুরি।
১. ট্রাপিজিয়ামের ক্ষেত্রফল নির্ণয়ের সূত্র
ট্রাপিজিয়ামের ক্ষেত্রফল বের করার জন্য সমান্তরাল বাহু দুটির দৈর্ঘ্য এবং তাদের মধ্যবর্তী দূরত্ব বা উচ্চতা জানতে হয়।
গাণিতিক ভাষায়, যদি সমান্তরাল বাহু দুটির দৈর্ঘ্য যথাক্রমে $a$ এবং $b$ হয় এবং তাদের উচ্চতা $h$ হয়, তবে:
২. ট্রাপিজিয়ামের পরিসীমা নির্ণয়ের সূত্র
ট্রাপিজিয়ামের চারটি বাহুর দৈর্ঘ্যের যোগফলই হলো এর পরিসীমা।
যদি চারটি বাহুর দৈর্ঘ্য যথাক্রমে $a, b, c$ এবং $d$ হয়, তবে:
বাস্তব জীবনে ট্রাপিজিয়াম
আমাদের চারপাশে অনেক বস্তুই ট্রাপিজিয়াম আকৃতির হয়ে থাকে। যেমন:
-
বাড়ির ছাদ বা টিনের চালের আকৃতি।
-
হাতব্যাগ বা লেডিস পার্স।
-
পপকর্ন ফেলার বাকেট বা ঠোঙা।
-
নৌকার পাল।
জ্যামিতির পরিিমিতি অংশে ট্রাপিজিয়াম একটি গুরুত্বপূর্ণ অধ্যায়। আশা করি, এই আলোচনা থেকে ট্রাপিজিয়াম কাকে বলে এবং এর গাণিতিক প্রয়োগ সম্পর্কে আপনারা স্পষ্ট ধারণা পেয়েছেন।